2장 . 3장 . 4장 내용 정리

벡터, 행렬, 텐서

1차원 배열: 벡터 (axis 0 = 0, axis 1 = 0, axis 2 = 4)

ex. [1, 2, 3, 4]

→ shape: (, 4) 

 

2차원 배열: 행렬 (axis 0 = 0, axis1 = 2, axis2 = 3)

ex. [[1, 2, 1],

       [3, 4, 1]]

→ shape: (2, 3)

 

3차원 배열: 텐서 (axis 0 = 2, axis 1 = 2, axis 2 = 3)

ex. [[[1, 2, 0],

       [3, 4, 0]],

      [[5, 6, 1],

       [7, 8, 1]]]

 

→ shape: (2, 2, 3)

 

2장. 파이토치 기본 실습(ipynb 코드)

https://colab.research.google.com/drive/1PcyLuqiID6n_Z_HgOSY4WBsdxNntbpwI?usp=sharing 

2장. 파이토치 기초.ipynb

3장. 머신러닝 핵심 알고리즘(ipynb 코드)

https://colab.research.google.com/drive/1kDtgh9pSUojeoeVSbeWaqTo-VIYPjuRl?usp=sharing 

3장. 머신 러닝 핵심 알고리즘.ipynb

4장. 딥러닝 시작

퍼셉트론은 다수의 신호를 입력받아 하나의 신호 출력 

→ 신호를 입력으로 받아 "흐름/안 흐름(1 또는 0)"의 정보를 앞으로 전달하는 원리로 작동

 

AND 게이트(선형적으로 분리)

OR 게이트(선형적으로 분리)

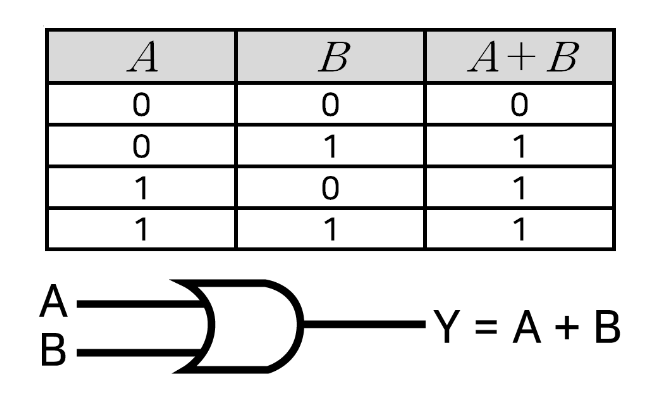
XOR 게이트(비선형적으로 분리)

: 입력 두 개 중 하나만 '1'일 때 작동하는 논리 연산

→ Sol. 입력층과 출력층 사이에 하나 이상의 은닉층을 두어 비선형적으로 분리되는 데이터에 대해 학습 가능하게 함

            :다층 퍼셉트론

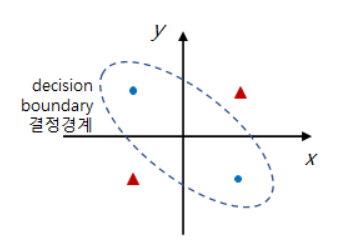
실제 계산 적용

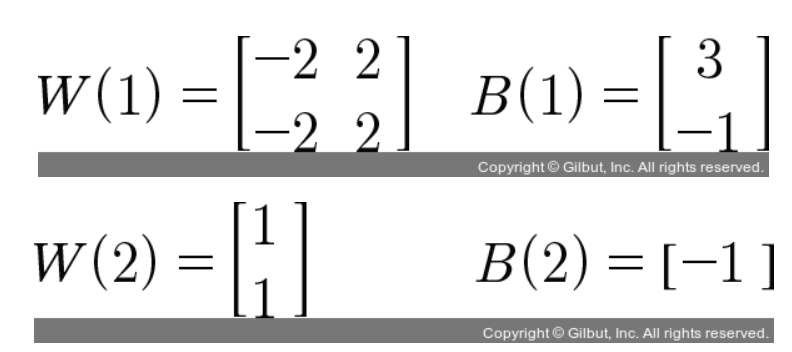
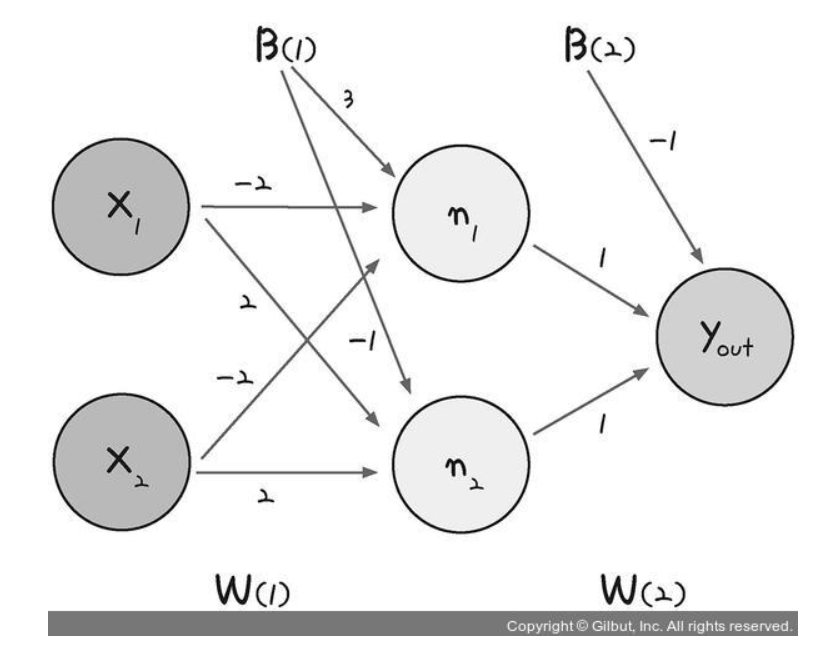
x1	x2	n1	n2	y_out	y(실제 우리가 원하는 값)
0	0	σ(0 * (-2) + 0 * (-2) + 3) ≈ 1	σ(0 * 2 + 0 * 2 - 1) ≈ 0	σ(1 * 1 + 0 * 1 - 1) ≈ 0	0
0	1	σ(0 * (-2) + 1 * (-2) + 3) ≈ 1	σ(0 * 2 + 1 * 2 - 1) ≈ 1	σ(1 * 1 + 1 * 1 - 1) ≈ 1	1
1	0	σ(1 * (-2) + 0 * (-2) + 3) ≈ 1	σ(1 * 2 + 0 * 2 - 1) ≈ 1	σ(1 * 1 + 1 * 1 - 1) ≈ 1	1
1	1	σ(1 * (-2) + 1 * (-2) + 3) ≈ 0	σ(1 * 2 + 1 * 2 - 1) ≈ 1	σ(0 * 1 + 1 * 1 - 1) ≈ 0	0

input: 4 * 2 . w1: 2 * 2 . w2: 2 * 1 . y & y_hat: 4 * 1

n1.n2: (4*2)*(2*2) = 4*2

y_out: (4*2)*(2*1) = 4*1

딥러닝 용어

입력층: 데이터(input data)를 받아들이는 층

은닉층: 모든 입력 노드로부터 입력값을 받아 가중합을 계산하고, 이 값을 활성화 함수에 적용해 출력층에 전달

출력층: 신경망의 최종 결과값이 포함된 층

가중치: 입력값의 연산 결과를 조정하는 역할

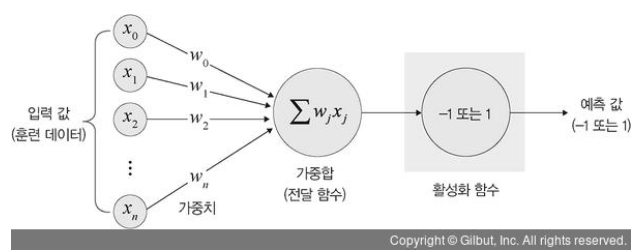
전달함수(가중합): 각 노드에서 들어오는 신호에 가중치를 곱해서 다음 노드로 전달되는데, 이 값들을 모두 더한 합계

활성화 함수: 전달함수에서 전달받은 값을 출력할 때 일정 기준에 따라 출력 값을 변화시키는 비선형 함수

→ sigmoid, tanh, Relu 등

 

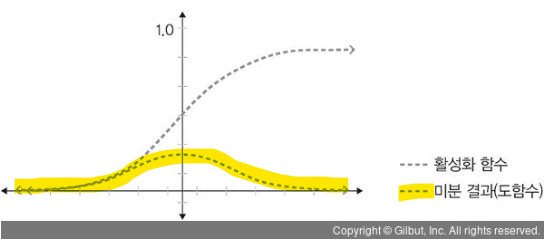
Sigmoid

: 선형 함수의 결과를 0~1 사이의 비선형 상태로 변형

: 딥러닝 모델의 깊이가 깊어지면서 '기울기 소멸 문제' 발생

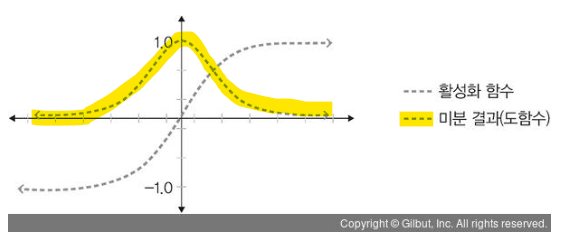
Tanh

: 선형 함수의 결과를 -1~1 사이의 비선형 상태로 변형

: Sigmoid보다는 낫지만, 여전히 기울기 소멸 문제 발생

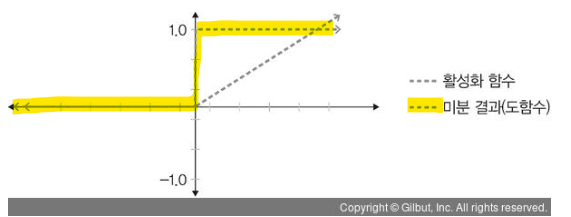
ReLU

: 경사 하강법에 영향을 주지 않아 학습 속도가 빠르고, 기울기 소멸 문제 발생 x

: 음수 값을 입력받을 경우 항상 0을 출력하기 때문에 학습 능력 감소

LeakyReLU

: 경사 하강법에 영향을 주지 않아 학습 속도가 빠르고, 기울기 소멸 문제 발생 x

: 음수 값을 입력받을 경우에 매우 작은 수 반환

Softmax

: 입력값을 0~1 사이에 출력되도록 정규화해 출력값들의 총합이 항상 1이 되도록 함

: 출력 노드의 활성화 함수로 많이 이용

 

손실함수

: 예측한 값과 실제 값의 차이가 얼마나 나는지 평가하는 지표

→ MSE(평균 제곱 오차), CEE(크로스 엔트로피 오차) 등

 

MSE: 실제값과 예측값의 차이를 제곱해 평균낸 것

CEE: 분류 문제에 원-핫 인코딩한 경우 사용하는 오차 계산법

 

ex.

실제 레이블: [1, 0, 1, 1]

모델의 예측 출력: [0.9, 0.2, 0.8, 0.95]

 

L(y, p): 교차 엔트로피 손실
y_i: 실제 레이블의 i번째 요소 (0 또는 1)
p_i: 모델의 예측 출력의 i번째 요소 (0에서 1 사이의 확률)

 

손실 계산:

1. 첫 번째 예제: y_i = 1, p_i = 0.9
   L(1, 0.9) = - (1 * log(0.9)) = -(-0.105) = 0.105

2. 두 번째 예제: y_i = 0, p_i = 0.2
   L(0, 0.2) = - (0 * log(0.2)) = -0

3. 세 번째 예제: y_i = 1, p_i = 0.8
   L(1, 0.8) = - (1 * log(0.8)) = -(-0.223) = 0.223

4. 네 번째 예제: y_i = 1, p_i = 0.95
   L(1, 0.95) = - (1 * log(0.95)) = -(-0.051) = 0.051

 

Total Loss = 0.105 + 0 - 0.223 + 0.051 = -0.067

 

순전파: 입력층 → 은닉층 → 출력층, 실제값과 유사한 값으로 예측값 계산하는 과정

역전파: 출력층 → 은닉층 → 입력층, 손실 값을 최소로하는 방향으로 가중치 업데이트하는 과정

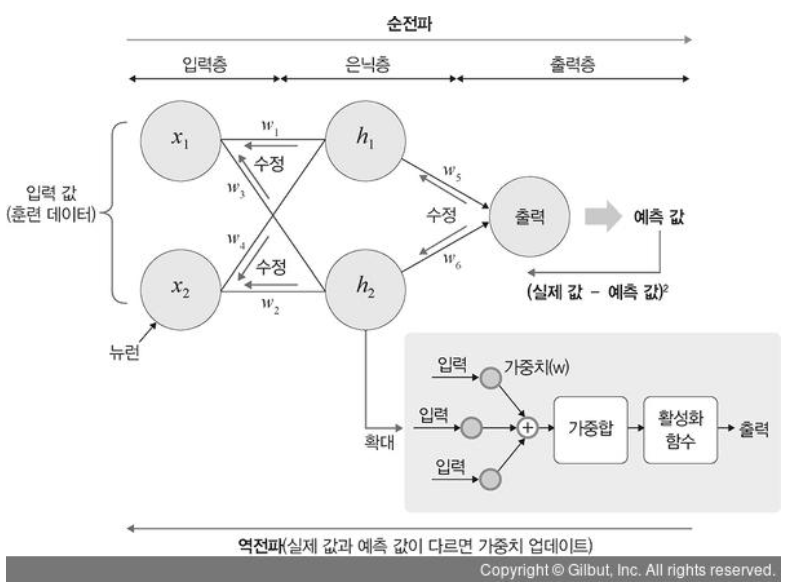
은닉층을 많이 쌓을수록 성능이 좋아지지만, 과적합이 발생할 수 있으므로 학습 과정의 일부 노드들을 학습에서 제외시키는 dropout을 적용하기도 한다

기울기 소실 문제를 해결하기 위해 ReLU함수를 이용하면 된다

경사 하강법

배치 경사 하강법: 전체 데이터셋에 대한 오류를 구한 후 기울기를 한 번만 계산해 모델의 파라미터 업데이트

→ 한 스텝에 전체 훈련 데이터셋을 이용하기 때문에 시간이 오래 걸림

 

확률적 경사 하강법: 임의로 선택한 데이터에 대해 기울기를 계산하는 방법으로 적은 데이터를 사용하므로 빠른 계산이 가능하지만, 배치 경사 하강법보다 성능이 안 좋을 수 있다

 

미니 배치 경사 하강법: 전체 데이터셋을 미니 배치(mini-batch) 여러 개로 나누고, 미니 배치 한 개마다 기울기를 구한 후 그것의 평균 기울기를 이용하여 모델을 업데이트해서 학습하는 방법

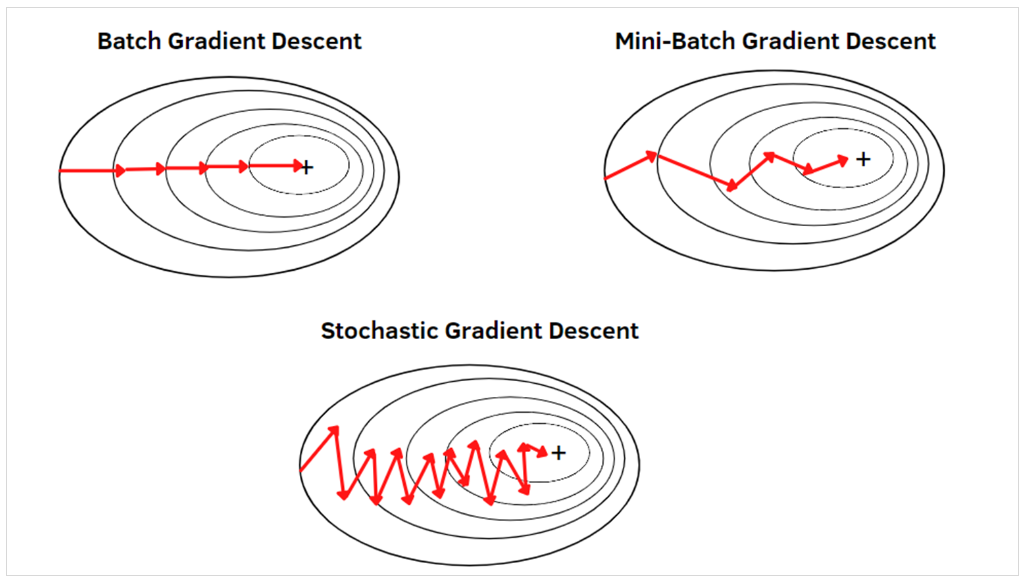
확률적 경사 하강법의 파라미터 변경 폭이 불안정한 문제를 해결하기 위해 학습 속도와 운동량을 조정하는 옵티마이저(optimizer)를 적용해 볼 수 있다

딥러닝 알고리즘

: 합성곱 신경망, 순환 신경망, 제한된 볼츠만 머신, 심층 신뢰 신경망