Linear Regression Model
: model의 출력이 연속적인 값을 가짐
: 연속되는 출력을 예측하기 위해 label(정답)이 있는 dataset을 사용

Linear Model
: 선형모델에서의 Hypothesis set H는 X(input feature)와 θ(model parameter)의
linear combination으로 구성

: 선형 모델이라고 해서 입력 변수 X에 대해서는 선형일 필요가 없음

선형 모델의 장점
- Simplicity : 모델이 단순해 성능 측정이 쉽고 해석이 간단함
- Generalization : 모델이 안정적인 성능 제공 가능(모델 변동이 심하지 않음)
Feature organization
: feature를 추출하는 과정도 매우 중요
: 의미 없는 feature를 사용할 경우 학습의 의미가 없어짐
: feature extractor를 통해 입력의 다양한 특징을 추출 가능
: 입력 feature로부터 θ(model parameter)와의 linear combination을 통해 Hypothesis 함수 구성

Linear Regression 예시
: 사용하는 data sample의 구성은 입력 x와 출력 y의 pair로 구성
: 여기서 y는 연속적인 값
Univariate problem
: 입력 변수가 1개인 문제
Multivariate problem
: 입력 변수가 2개 이상인 문제

Linear Regression Framework
: 주어진 입력에 대해 출력과의 선형적인 관계를 추론하는 문제
고려해야할 3가지 요소
- 어떤 predictor를 이용할 것인지 → Hypothesis class / ex. Univariate linear model
- predictor의 성능은 얼마나 좋은지 → Loss Function / ex. MeanSquaredError(MSE) 최소화
- 최고의 predictor를 만드려면 어떻게 해야하는지, 어떻게 파라미터를 구하는지 → Optimization algorithm / ex. Gradient descent algorithm, Normal equation

Linear regression: parameter optimization
: 모델의 좋은 성능을 위해 파라미터를 최적화해야 함
: 모델 파라미터가 달라짐에 따라 주어진 데이터를 fitting 하는 과정에서 오차가 발생할 수 있음
: 여기서 θ_0는 offset(편향)임
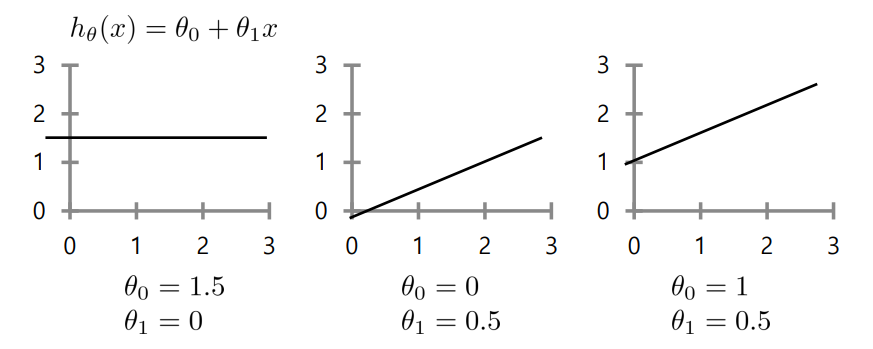
L2 cost function (Goal : minimizing MSE)
: 선형모델의 목적은 cost function(손실 함수)을 최소화하는 θ_0, θ_1을 찾는 것
: 가장 데이터에 fitting 하는 선형 모델을 찾게 해줌
: cost function == J(θ_0, θ_1)
→ 세타들에 의해 cost function이 0이 되는 값의 확보가 목표

: loss function이 가장 낮을 때 θ_0과 θ_1이 가장 최적화된 모델임을 알 수 있음

Optimization -Matrix representation in data
parameter optimization → cost function을 최소화 하는 θ를 구하는 과정
- X_m은 1 * (d+1) 차원임에 유의 → offset인 θ_0(b)를 포함시키기 때문에 X_m은 d+1개
- parameter도 (d+1) 차원임에 유의 → offset인 θ_0(b)부터 θ_d까지 존재하기에 parameter도 d+1개
- y: label(정답) / Xθ: score(모델 출력)
: learning parameter θ는 X와 선형 결합을 통해 Xθ(score)로 이루어지게 됨

Optimization -Getting a solution θ
: parameter θ(가중치)를 최적화하는 과정으로 분석적 해 구하기
: 손실함수를 θ(가중치)에 대해 미분했을 때 0이라는 식을 통해 손실함수를 최소화하는 θ를 구하는 방식
: Least Square Problem(과정)
: Normal Equation(방정식)
problem)
: data의 샘플 숫자가 늘어나는 경우 비효율적임
→ 전치행렬 등을 구하는 과정에서 너무 큰 복잡도가 발생하여 효율적이지 못하며 전치행렬이 없는
데이터 샘플도 존재하기 때문
solution)
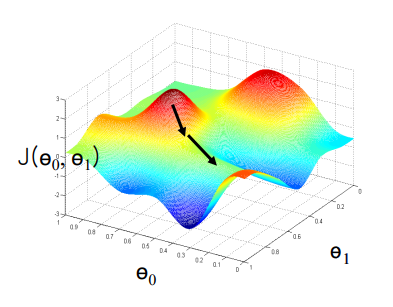
: gradient descent를 통해 최적의 paramter를 구하기

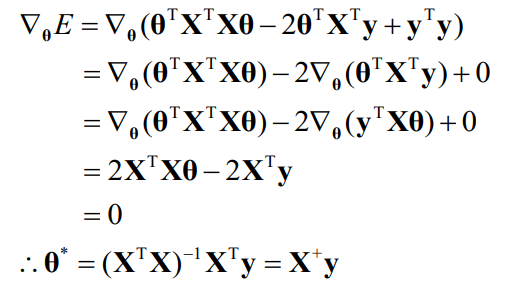
Iterative optimization by gradient descent
Gradient: 해당 함수의 변화하는 정도를 표현하는 값
: error surface에서 최소인 포인트(gradient가 0인 지점)를 찾아나가는 반복과정을 통해 파라미터 θ를 바꾸며 gradient가 0인 지점을 찾아나감
: 하강 기울기가 가장 큰 쪽으로 반복적으로 내려가며, error surface에서 가장 낮은 지점을 찾아감
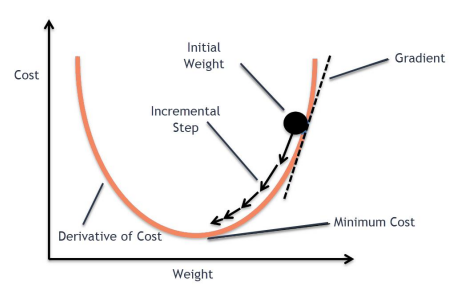
아래의 식처럼 최적의 파라미터를 찾을 때까지 파라미터를 업데이트 함
여기서, a는 학습률이고 파라미터의 업데이트 속도를 조절하는 역할

a가 큰 경우
: weight 최소 지점에 수렴이 어려움
a가 작은 경우
: weight 최소 지점 수렴까지 너무 오랜 시간이 걸림
Error surface
Global optimum
: error surface에서 가장 최소인 값을 갖는 지점
Local optimum
: 특정 구역에서는 최소이지만 전체 영역에서는 최소가 아닌 지점
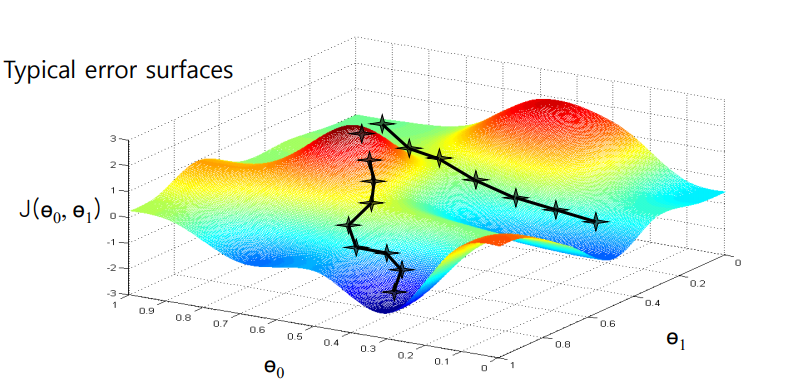
아래 그래프와 같은 Local Minima와 Saddle points를 해결하기 위해 stochastic gradient descent, mini batch 방식을 이용할 수 있음

'실습 & 활동 > LG Aimers' 카테고리의 다른 글
| Module 3. 지도학습 (분류/회귀) - Advanced Classification (0) | 2023.01.24 |
|---|---|
| Module 3. 지도학습 (분류/회귀) - Linear Classification (0) | 2023.01.19 |
| Module 3. 지도학습 (분류/회귀) - Gradient Descent (0) | 2023.01.17 |
| Module 3. 지도학습 (분류/회귀) - SL Foundation (0) | 2023.01.15 |
| Module 1. AI 윤리 (0) | 2023.01.02 |



